Listrik statis adalah suatu kumpulan muatan listrik dalam jumlah
tertentu yang tidak mengalir atau tetap (statis), tapi jika terjadi
pengosongan muatan akan memakan waktu yang cukup singkat.
Atau dapat didefinisikan : suatu fenomena kelistrikan yang dimana
muatan listriknya tidak bergerak dan biasanya terdapat pada benda yang
bermuatan listrik.
Salah satu contoh peristiwa timbulnya listrik statis yaitu penggaris
plastik yang digosok-gosokanan pada rambut kering, lalu di dekatkan pada
kertas yang sudah dirobek kecil-kecil maka kertas tersebut akan
tertarik oleh penggaris jadi seolah-olah penggaris seperti magnet yang
dapat menarik benda, padahal itu merupakan adanya listrik statis. Kenapa
bisa seperti itu? sebab serpihan kertas yang asalnya bermuatan netral
akan terinduksi akibat tertarik muatan negatif yang terdapat pada
penggaris.
Adapun beberapa contoh lain dari listrik
statis yang dapat ditemui dalam rutinitas sehari-hari, yang diantaranya
sebagai berikut ini:
- Saat kita menyisir rambut maka tanpa kita sadari terkadang rambut kita akan terbawa berdiri sendiri siring dengan gerakan sisir. Hal seperti ini dapat terjadi karena adanya interaksi muatan antara sisir dengan rambut kita.
- Kain sutra yang digoso-gosok pada batang kaca. Pada peristiwa ini benda tersebut akan bereaksi saling tarik-menarik. Kenapa bisa seperti itu? setelah keduanya saling digosok-gosokan akan terjadi loncatan elektron dari batang kaca ke kain sutera sehingga mengakibatkan batang kaca bermuatan positif sedangkan kain sutera bermuatan negatif, hal ini hampir sama seperti pada penggaris yang digosok-gosokan pada rambut.
- Penggaris plastik yang digosok-gosokan pada kain woll. Kedua benda tersebut umumnya memiliki muatan netral, tapi saat keduanya digosok-gosokan akan terjadi loncatan elektron yang berasal dari kain woll ke penggaris plastik dan penggaris plastik menjadi bermuatan negatif sedangkan kain woll menjadi bermuatan positif.
- Ketika mendekatkan tangan ke layar TV yang baru dimatikan. Pada peristiwa ini jika di perhatikan bulu-bulu atau rambut yang ada pada tangan akan berdiri, hal seperti itu diakibatkan karena adanya listrik statis.
A. Gaya Coulomb

Bila dua buah muatan listrik dengan harga q1 dan q2,
saling didekatkan, dengan jarak pisah r, maka keduanya akan saling
tarik-menarik atau tolak-menolak menurut hukum Coulomb berikut :
“Besar Gaya
Interaksi(tolak menolak/tarik menarik) antara dua buah muatan berbanding
lurus dengan besar muatan-muatannya dan berbanding terbalik dengan
kuadrat jarak antara kedua muatan”.
F = Gaya interaksi (N)
k = konstanta coulomb (9.109 Nm^2/C^2)
q = muatan listrik (C)
r = jarak antara kedua muatan listrik (m)
Interaksi Muatan
Interaksi antara dua muatan, bila muatannya sejenis akan tolak
menolak, bila berbeda muatannya akan tarik menarik. Dan arah gaya tolak
menolak atau tarik menarik seprti pada gambar dibawah
Konstanta pembanding (“k”) harganya tergantung pada tempat dimana muatan tersebut berada.Bila pengamatan dilakukan diruang hampa/udara; besar “k” dalam sistem SI adalah k= 9 x 10 9 Nm2/Coulomb2
e0 = permitivitas udara atau ruang hampa.
= 8,85 x 10-12 Coulomb2 / newton m2
Untuk medium selain udara, maka harga k juga lain sebab tergantung dari permitivitasnya.
Contoh Soal :
Dua buah muatan listrik q1 = – 1,0μC dan q2 = + 2,0μC berjarak
0,30 meter. Tentukan besar gaya interaksi kedua muatan tersebut !
Karena F adalah vektor, maka bila gaya resultan yang disebabkan oleh 3 titik muatan, penjumlahannya juga memenuhi aturan vektor.
B. Medan Listrik
Dalam ruang disekitar benda bermuatan listrik A, kita jumpai beberpa
gejala. Sebagai contoh benda bermuatan lain B dapat bergerak menjauhi
atau mendekati A ( Gambar 1.). Gejala ini disebabkan bekerjanya sutu
gaya pada benda bermuatan apa saja yang diletakkan dalam ruang di
sekitar benda bermuatan A. Kita sebut gejala dalam ruang di sekitar
suatu benda bermuatanlisrik ini medan listrik.
Gambar 1 : gaya yang bekerja pada muatan-muatan yang diletakkan dalam ruang disekitar benda bermuatan A
Jadi Medan Listrik adalah ruang di
sekitar benda bermuatan listrik dimana benda-benda bermuatan listrik
lainnya dalam ruang ini akan merasakan atau mengalami gaya listriArah
Medan Listrik
Arah Medan Listrik
Medan Listrik dapat kita gambarkan dengan garis-garis khayal yang
dinamakan garis-garis medan (atau garis-garis gaya listrik). Dapat anda
lihat pada gambar 2 dan gambar 3 bahwa garis-garis medan radial
keluar menjauhi muatan positif dan radial kedalam mendekati muatan
negative
Kuat Medan Listrik
Kuat Medan Listrik adalah besaran yang menyatakan gaya coloumb per satuan muatan di suatu titik.
Misalnya di titik P, Lihat gambar.
– Jika titik P di beri muatan , maka muatannya dinamakan muatan penguji (q), dan selalu bermuatan positif
– Q = Sumber muatan
– Arah Kuat Medan Listrik (E), searah dengan arah gaya (F)
Secara matematik kuat medan Listrik dirumuskan :
Karena Besar gaya Columb antara muatan sumber Q dan muatan uji q, maka Rumus Kuat Medan Listrik adalah sebagai berikut :
dengan : E = kuat medan listrik (N/C)
Q = muatan sumber (C)
r = jarak muatan uji trhadap muatan sumber (m)
k = konstanta = =9×109 Nm2/C2
ε0 = permitivitas listrik vakum = 8,85 . 10-12 C2/Nm2
C. Energi Potensial Listrik
Hukum kekekalan energi
memungkinkan kita memecahkan persoalan-persoalan tanpa perlu mengetahui
gaya secara rinci. Sebagai contoh gaya gravitasi menarik suatu benda
menuju ke permukaan bumi. Baik gaya gravitasi Fg maupun kuat medan
gravitasi (percepatan gravitasi=g) berarah vertikal ke bawah.
Jika mengangkat sebuah benda melawan gaya gravitasi bumi, itu berarti
kita melakukan usaha pada benda, dan sebagai akibatnya energi potensial
gravitasi benda bertambah
( gambar 1)
Konsep energi juga berguna dalam listrik. Gaya
listrik F yang dikerjakan pada suatu muatan Uji positif q’ oleh suatu
muatan negatif adalah mengarah ke muatan negatif. Vektor kuat medan
listrik E= F/q’, juga mengarah ke muatan negatif.
Untuk menggerakkan muatan uji menjauhi muatan negatif, kita harus
melakukan usaha pada muatan uji. Sebagai akibatnya energi potensial
listrik muatan uji bertambah (gambar 2).
Gambar 1 Gambar 2
Konsep energi potensial listrik, mirip dengan konsep energi potensial garavitasi. Untuk itu kita akan menurunkan rumus Energi Potensial Listrik sebagai berikut :

Usaha yang dilakukan gaya (Fw), untuk memindahkan muatan penguji +q’, dari titik P ke Titik Q adalah W =- Fw . S = -Fw.Δr=-F.(r2-r1)
W adalah besaran skalar, gaya F diberi tanda (-) negatif karena gaya
Coulomb berlawanan arah dengan arah perpindahah Fw=Fq = gaya Coulomb.
W = -k.Q q’/r1 2 x (r2-r1) = – kQ.q’/r1.r2 (r2-r1)
W = -k Q.q'(1/r1 – 1/r2)= k Q.q'(1/r2-1/r1)
W = k Q.q'(1/r2-1/r1) = Δ EP = EP2 – EP1
Jadi usaha yang dilakukan W= pertambahan energi Potensial.
Kesimpulan : Energi Potensial Listrik adalah usaha yang dilakukan gaya Coulomb, untuk memindahkan muatan uji +q’ dari suatu titik ke titik lainnya.
Jika titik Q, berada di jauh tak terhingga,sehingga r2= ˜ dan 1/r2=0
maka Energi Potensial Listrik dapat dirumuskan sebagai berikut: Energi
Potensial Listrik dari dua muatan Q dan q’ adalah :
E= Energi Potensial Listrik satuannya Joule
k = Konstanta = 9.109 N C-2 m2, r= jarak (m)
Q + muatan sumber, q’= muatan uji (Coulomb)
D. Potensial Listrik (V)
Potensial listrik adalah energi potensial per satuan muatan penguji ,
rumus potensial listrik sebagai berikut : V = Ep /q’ atau seperti
pada gambar berikut
V = k Q/r
V = Potensial Listrik (Volt)
k = Konstanta Listrik = 9.109 NC-2 m2
Q = Muatan sumber (Coulomb)
r = jarak dari muatan sampai titik P
Contoh Soal :
1. Sebuah usaha diperlukan untuk memindahkan sebuah
muatan positif sebesar 10 C yang potensialnya 10 Volt dari sebuah titik ke
titik lain yang potensialnya sebesar 60 Volt. Besar usaha tersebut adalah . . . Penyelesaian:
2. Jika medan listrik antara dua plat paralel sebesar 2400 N/C dan jarak antar kedua plat 0,5 cm, maka beda potensialnya adalah...
Pembahasan:
V = E . d
V = 2.400 N/C . 0,005 m = 12 V
Pembahasan:
V = E . d
V = 2.400 N/C . 0,005 m = 12 V
E. Hukum Gauss
Hukum Gauss merupakan hukum fisika lainnya yang menjelaskan keterkaitan antara muatan listrik dengan medan listrik. Hukum Gauss dirumuskan oleh Carl Friedrich Gauss (1777-1855), fisikawan teoritis dan matematikawan berkebangsaan Jerman.
Medan listrik yang ditimbulkan oleh satu atau beberapa muatan listrik dapat dihitung dengan mudah menggunakan hukum Coulomb, tetapi perhitungan menjadi lebih rumit jika yang ditentukan adalah medan listrik yang dihasilkan oleh suatu distribusi muatan listrik. Hukum Gauss menyediakan cara yang lebih mudah untuk menentukan medan listrik yang dihasilkan oleh suatu distribusi muatan listrik. Selain itu, jika diketahui medan listrik maka hukum Gauss dapat digunakan untuk menentukan distribusi muatan listrik yang menghasilkan medan listrik tersebut.
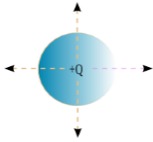
Tinjau sebuah muatan listrik positif yang berada di pusat bola sebagaimana tampak pada gambar di samping. Apabila jari-jari bola adalah R maka kuat medan listrik yang dihasilkan muatan tersebut di seluruh permukaan bola adalah E = k Q / R2 dan luas permukaan bola adalah A = 4 π R2.
Untuk memvisualisasikan medan listrik maka digambarkan garis-garis medan listrik tetapi pada gambar hanya diwakili empat garis medan listrik. Muatan listrik positif karenanya garis-garis medan listrik digambarkan keluar dari pusat bola di mana muatan listrik berada dan masing-masing garis medan listrik tegak lurus dengan permukaan bola yang dilewatinya. Semakin jauh dari muatan listrik, medan listrik semakin kecil sehingga jarak antara garis-garis medan listrik juga semakin jauh.
Hukum Gauss merupakan hukum fisika lainnya yang menjelaskan keterkaitan antara muatan listrik dengan medan listrik. Hukum Gauss dirumuskan oleh Carl Friedrich Gauss (1777-1855), fisikawan teoritis dan matematikawan berkebangsaan Jerman.
Medan listrik yang ditimbulkan oleh satu atau beberapa muatan listrik dapat dihitung dengan mudah menggunakan hukum Coulomb, tetapi perhitungan menjadi lebih rumit jika yang ditentukan adalah medan listrik yang dihasilkan oleh suatu distribusi muatan listrik. Hukum Gauss menyediakan cara yang lebih mudah untuk menentukan medan listrik yang dihasilkan oleh suatu distribusi muatan listrik. Selain itu, jika diketahui medan listrik maka hukum Gauss dapat digunakan untuk menentukan distribusi muatan listrik yang menghasilkan medan listrik tersebut.

Tinjau sebuah muatan listrik positif yang berada di pusat bola sebagaimana tampak pada gambar di samping. Apabila jari-jari bola adalah R maka kuat medan listrik yang dihasilkan muatan tersebut di seluruh permukaan bola adalah E = k Q / R2 dan luas permukaan bola adalah A = 4 π R2.
Untuk memvisualisasikan medan listrik maka digambarkan garis-garis medan listrik tetapi pada gambar hanya diwakili empat garis medan listrik. Muatan listrik positif karenanya garis-garis medan listrik digambarkan keluar dari pusat bola di mana muatan listrik berada dan masing-masing garis medan listrik tegak lurus dengan permukaan bola yang dilewatinya. Semakin jauh dari muatan listrik, medan listrik semakin kecil sehingga jarak antara garis-garis medan listrik juga semakin jauh.
Fluks listrik yang menembus permukaan bola dihitung menggunakan rumus berikut :
Keterangan :
Φ = fluks listrik, Q = muatan listrik, k = 9 x 109 N m2/C2, εo (permitivitas ruang hampa) = 8,85 x 10-12 C2/N m2, π = 3,14.
Berdasarkan persamaan ini disimpulkan fluks listrik (Φ) yang melewati suatu permukaan berbentuk bola, sebanding dengan jumlah muatan listrik (Q) di dalamnya dan tidak bergantung pada jari-jari bola (R).
Berdasarkan persamaan ini disimpulkan fluks listrik (Φ) yang melewati suatu permukaan berbentuk bola, sebanding dengan jumlah muatan listrik (Q) di dalamnya dan tidak bergantung pada jari-jari bola (R).














